在《了解一致性hash算法》中介绍了一致性hash ring的实现算法。
但是切割hash环的时候,遇到一个思考题:
在数字环上随机落N个点,把环切分成N个区间,原点要算一个切分点吗?如果算,就只产生N-1个随机数就可以了,如果不算,要产生N个随机点。
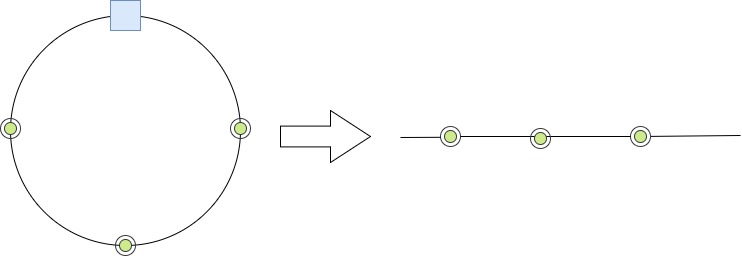
为什么会产生这个疑问?如上图,把hash用三个绿色点分割了三段。如果把环从蓝色的0点打开,变成右边的直线。直线被分成了四段。随机分割直线四段,肯定用右边的方法,为啥切割hash环就用左边的方法呢?
最终owen认为,还是要把0点当作一个已经切分过的node来处理,因为每次产生的随机数,都是按照右边展开的直线的空间来落点,分割直线的。环只是一个让人容易理解的模型,真正实现时还是按照一维来生成随机点的。否则,跨过0点的区间段,会是其他区间的二倍。
在工程实践中,为什么也没发生不均匀的问题,用的好好的呢?
有两个原因:
一、引入了虚节点,分割的区间太多,即使跨0点有两个区间段,也在程序接受的误差范围内。
二、由于是随机落点,分割的区间段大小不一,检测程序也会控制各实节点间的误差符合项目要求。
顺便说一下,把0点作为一个已切分的点还有个好处:不用特别考虑跨0区间key的归属情况,程序容易写。
总结
把零点算作一个node,产生N-1个节点切分hash环;
实际切分的区间是否均匀,要靠检测程序来检查,不能只依赖理论推断。
在数字环上随机落N个点后,发现0点所在的区间长度,要比其他段长,是其他段的两倍。
随机落点的算法是:在环的区间范围[0,n)的区间随机产生N个整数,然后落点。
该问题导致随机的N个点并不均衡,实际上0所在的服务器会有更大的负载。如果虚拟节点多过多,会掩盖这个问题,也不会造成太大的麻烦。
如何解决?
在0点也插入一个节点,分为N+1个区间,每个区间就都均衡了。
为什么?
把hash ring想象成为一条线段,在线段上随机落N-1个点,那么这N-1个点给线段分割为N段左闭右开的区间,本质上和hash ring的算法是一样的。如果落得点多,每段线段长度的期望相同,都是n/N。在hash ring算法中,0所在的点被包含在了首位两个段中,所以期望是其他段的两倍。
如果以其他的点为起始点,以随机数偏移落点,和上面的情况类似,只是把圆按照偏移转了个相应的角度,不影响算法的结果。起始点所在的区间也是其他区间的二倍。
原因是和落点的随机算法有关,因为每次落点的随机数,都是以起始点开始,到终点结束的范围内产生随机数。在这个一维空间内产生随机点的均匀程度,是相对于起止点两点的范围产生,在0点和环上对应,相当于已经落了一次点。
以上只是由想法退出,并没有严格的推论,如果有人知晓,烦请指正。
附模拟程序和实验结果,在[0,1000000)的hash环上,随机落10,000个点,每次落点的位置都是[0,1000000)区间产生的随机整数所在点的坐标,分为10,000个段,平均每段长度100,执行100次,发现最大长度分布都在200左右,最小长度都在100左右。
import random
from bisect import bisect_left
ITEMS = 1000000
NODES = 100
node_stat = [0 for i in range(NODES)]
ring = []
hash2node = {}
for n in range(NODES):
h = random.randint(0, 10000)
ring.append(h)
hash2node[h] = n
ring.sort()
print len(ring)
for item in range(ITEMS):
h = random.randint(0, 10000)
n = bisect_left(ring, h) % (NODES)
node_stat[hash2node[ring[n]]] += 1
print sum(node_stat), node_stat, len(node_stat)
_ave = ITEMS / NODES
_max = max(node_stat)
_min = min(node_stat)
print(“node_stat[0]: %d” % node_stat[0])
print(“node_stat[-1]: %d” % node_stat[-1])
print(“Ave: %d” % _ave)
print(“Max: %d\t(%0.2f%%)” % (_max, (_max - _ave) * 100.0 / _ave))
print(“Min: %d\t(%0.2f%%)” % (_min, (_ave - _min) * 100.0 / _ave))